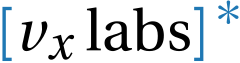The wonderful Emacs Org mode is the basis for the largest part of my personal knowledge management system. However, as I’ve mentioned before, mobile accessibility is its weakest point. In this post, I’m going to explain my possibly unconventional new solution to the important requirement I mentioned in that note-taking post: Ideally, I would have easy access to my complete org database and any related files. As you can easily deduce from the title of this post, the solution involves converting all of my org database into docx files, with the main motivation that the Dropbox mobile app has excellent support both for the fast previewing and searching through the contents of docx files, while it has none of that sort of support for .

This post is reproduced here with permission from The OrgMode ExoCortex. org-roam v2, which was recently released, removed the update database on idle functionality (which I coincidentally contributed) as part of its simplification. I agree with this removal, as I think it makes the most sense to keep the org-roam core as simple as possible. That being said, being able to have the org-roam database update only when Emacs is idle can be helpful for some folks, like me, who C-x C-s quite often and notice a few hundred millisecond blocking delay on files of a thousand or more lines.

Welcome to open source vxlabs software development handbook. It contains a number of best practices for building software, generally web-based, using Python on the backend and TypeScript for the frontend. However, most of the guidelines are more broadly applicable. Important note: These are only guidelines. They were never meant to be applied dogmatically. They are great when you are starting fresh, and their intentions are good, but please do understand and adapt to your situation.

Recently the great support folks at FastMail helped me to debug a rather irritating issue where emails that had languished in my inbox for too long, and were then processed by me to end up in the Archive folder, would get the date of archival assigned as the main email date, instead of the date of arrival. For example, an email with a date in November of 2020 would get a new date of say February 21, 2021, if that’s the date that I finally got around to it and moved it to the Archive folder.

On the various and different platforms where I use Emacs and GnuPG encryption, I’ve traditionally always had a bit of a struggle setting up a suitable mechanism for private key passphrase entry, or pinentry. Recently, I landed upon this extremely easy-to-setup and reliable solution where Emacs and GnuPG can be configured so that Emacs requests the passphrase via its standard minibuffer password entry mechanism, and then passes this through to GnuPG.

Recently, as I replaced more of my Emacs-helm configuration with counsel and ivy, I noticed that ivy-switch-buffer, when augmented by ivy-rich, was not showing the directories of the buffers it was listing. After some Lisp spelunking, I discovered that it was because ivy-rich relies on the presence of either the projectile package, something I do not wish to have in my Emacs configuration, or on project.el, which I also do not use.

Welcome to the first entry in a new series that’s probably going to stop with this first entry, or maybe not. The series is called Charl’s Unwritten Rules of Software Development, or cursd. I am also planning another series called Charl’s Unwritten Rules of Applied Machine Learning that is on its part probably going to remain in the planning stage, or maybe not. In this first CURSD post, I would like to document my hitherto unwritten rule for ordering your TypeScript (or JavaScript) import groups.